Онлайн калькулятор. Калькулятор использует методы регрессии для аппроксимации функции одной переменной. Mar 1, 2017 - Обычно для аппроксимации гиперболической функцией методом. Поэтому привожу простую программу на Python, для классической. Аппроксимация функций полиномом методом наименьших квадратов. Алгоритм реализован в виде программы на языке С, которую вы можете скачать. Аппроксимации и восполнения функций. Эти программы универсальны и их применение не ограничено сплайн-аппроксимацией.

1. Аппроксимация Функции Программа Скачать
2. Аппроксимация Функций Программа

Вы научились анализировать стабильность качества процессов, продукции. Умеете находить точечные и интервальные значения средних, характеристик разброса. Но этого мало! Обязательно появится желание улучшить процессы (например, улучшить качество продукта, снизить затраты, сократить время обработки и т.п.). Но для этого нужно воздействовать на процесс, причем воздействие это желательно рассчитать заранее так, чтобы изменить процесс или продукт в нужном направлении, не испортить. А как это сделать, если не знаешь 'силы влияния' того или иного управляющего воздействия на контролируемый результат?

Или другая часто встречающаяся задача: с какой точностью нужно поддерживать режимы процесса, чтобы получить разбросы характеристик продукта на выходе в заданных пределах? Для этого нужно знать, как взаимодействуют входные и выходные параметры процесса. Другими словами, нужно находить причинно-следственную связь между входными и выходными параметрами. Основная задача аппроксимации - построение приближенной (аппроксимирующей) функции, в целом наиболее близко проходящей около экспериментальных значений (точек) показателя качества. Такая задача возникает при наличии погрешности в исходных данных, когда нецелесообразно проводить функцию точно через все точки или при желании получить упрощенное математическое описание сложной или неизвестной зависимости.

В последствии эта зависимость может быть использована при управлении процессами для расчета прогнозируемых значений показателя качества. Программа 'Аппроксимация' позволит получить уравнение связи выходных величин процесса от входных с учетом различных значений весовых коэффициентов. В программе реализовано нахождение коэффициентов следующих аппроксимирующих функций.

Под аппроксимацией понимают метод, состоящий в замене исходного объекта более простым объектом, но близким в определенном смысле. Аппроксимация начальной функции более простыми данными часто значительно упрощает решение задачи по оптимизации. При решении экономических задач аппроксимация в большей степени применяется для укрупнения показателей моделируемых объектов экономической жизни.

Для решения данных задач может применяться программный продукт Microsoft Excel 1. Программа Microsoft Excel, является лидером на рынке программ обработки электронных таблиц, развивает тенденции развития в этой области. При помощи этого продукта можно анализировать большие массивы данных. В Excel можно применять более четырехсот статистических, финансовых, математических и других специализированных функций, соединять различные табличные данные посредством и между собой, выбирать случайно выбранные форматы предоставления данных, создавать различные структуры. С помощью Microsoft Excel и аппроксимирующих функций в нем, мы довольно быстро, не затрачивая на это большого количества усилий, можем построить наглядные изменения производительности труда, а следовательно эффективности предприятия, с истечением времени. Отсюда следует, что с помощью аппроксимации можно сделать прогноз о поведении исследуемой системы в будущем, и возможность выбрать оптимальное ее развитие.

При выборе аппроксимирующих функций следует исходить из конкретной задачи экспери- мента. Обычно, чем более легкое уравнение используется для аппроксимации, тем более приближенное значение мы получим при описании зависимости. Поэтому важно просчитывать, насколько существенны отклонения и чем они обусловлены. При описании зависимостей определенных значений можно добиться гораздо увеличенной точности, используя какое-либо более сложное, параметрическое уравнение.

Однако нет ника- кого смысла стремиться к максимальной точностью передать появившиеся отклонения величин в конкретных рядах данных эксперимента. Гораздо важнее найти общую закономерность, кото- рая в данном случае наиболее правильно и с позволяющей точностью выражается именно двухпараметрическим уравнением степенной функции 1. В Microsoft Excel аппроксимация данных для эксперимента осуществляется путем построения их графиков (x — отвлеченные величины) или точечного графика (x — имеет конкретные значения) с последующим подбором подходящей аппроксимирующей функции (линии тренда). К примеру, нужно проиллюстрировать графически зависимость производительности труда, в течение года.

Производительность труда — основной показатель экономической эффективности производства предприятия и каждой организации. Выявление резервов и достижение увеличения производительности труда должно опираться на комплексный экономический анализ работы предприятия.

Анализ производительности труда позволяет определить эффективность использования на предприятии трудовых ресурсов и постоянно располагаемого рабочего времени. Рост производительности труда означает: увеличение производства, одновременно с уменьшением понесенных издержек 3. Проиллюстрируем применение различных вариантов аппроксимации на основе таблицы 1, в которой содержатся данные о количестве сотрудников некоторой компании и количестве произведенной продукции.

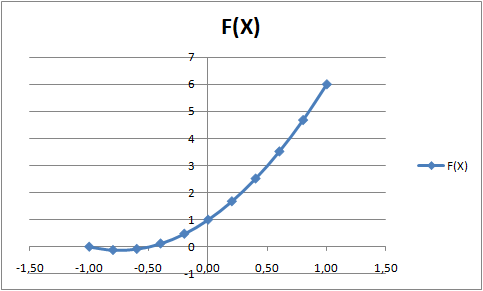
Необходимо в ыявить зависимость на предприятии, между количеством сотрудников и производством продукции, с истечением определенного периода времени. Данные о производительности компании Временная база: Количество сотрудников Производство продукции Общее количество Количество рабочих 2005 — 2006 1200 8 — 2007 1198 7 — 2009 1242 8 — 2010 900 700 38 В Microsoft Excel можно построить график и для него добавить линию тренда. Это и послужит примером аппроксимирующей формулы.

Возможны следующие варианты аппроксимирующих функций: 1. Линейная: (остальные формулы набери тоже с помощью редактора формул). Обычно применяется в простейших наглядных случаях, когда данные в эксперименте возрастают или убывают с большей скоростью. Пример линейной аппроксимации 2.

Полиномиальная:, до шестого порядка включительно (n≤6), где — константы. Применяется для описания данных в эксперименте, которые попеременно возрастают и убывают. Степень полинома определяется количеством максимумов или минимумов кривой. Полином второй степени можно описать только либо один максимум, либо один минимум, полином третьей степени может иметь одну или две экстремальных значения, четвертой степени — не более трех значений и т.

Пример полиномиальной аппроксимации 3. Логарифмическая:, где и — константы, — функция натурального логарифма. Функция используется для описания данных в эксперименте, которые сначала быстро растут или убывают, а затем постепенно балансируются. Пример логарифмической аппроксимации 4. Степенная:, где и — константы. Аппроксимация степенной функцией применяется для данных в эксперименте с постоянно увеличивающейся (или убывающей) скоростью роста. Данные не могут иметь нулевых или отрицательных значений.

Пример степенной аппроксимации 5. Экспоненциальная:, где и — константы, — основание натурального логарифма. Применяется для описания данных в эксперименте, которые быстро растут или убывают, а затем постепенно сбалансируются. Часто ее применение вытекает из теоретических наглядностей 2. Пример экспоненциальной аппроксимации Следовательно, с помощью формул аппроксимации мы более точно можем определить зависимость количества произведенной продукции от количества сотрудников на предприятии. С их помощью мы наглядно изучили, решение задачи. Исходя из вышеперечисленных графиков получаем: между количеством сотрудников и объемом выпускаемой продукции, по статистике существует прямая связь, так как с увеличением количества рабочих, увеличивается и количество изготавливаемой продукции и наоборот 3.

Аппроксимация Функции Программа Скачать

Таким образом, выбирая метод аппроксимации, мы всегда идем на принятие и понимание поставленных целей: решаем, в какой вероятности в данном случае более логично и применительно «пожертвовать» деталями и, соответственно, насколько соразмерно следует выразить зависимость сопоставляемых переменных. Наряду с выявлением закономерностей случайных отклонений в эксперименте аппроксимация позволяет также решать много других важных задач. Среди основных задач, решаемых с помощью аппроксимации, можно выделить следующие: поиск неизвестного значения зависимой переменной путем интерполяции ( оценки значения неизвестной величины, находящейся между двумя известными величинами) или экстраполяции ( распространение выводов, сделанных относительно некоторой части объектов на всю совокупность данных объектов); формализация полученной зависимости. Почти каждый из выше изложенных трендов или кривых роста имеет под собой определенно заложенный смысл. Линейные тренды характеризуют явления, в которых наблюдательно показанная величина протекает линейно. Экспоненциальные тренды существуют там, где изучаемая величина, имеет экспоненциальную или также можно сказать непрерывную (лавинообразную) динамику. Логарифмические тренды помогают описать степень насыщенности рынка.

Аппроксимация Функций Программа

Полиномиальные тренды предоставляют возможность описать при помощи различных полиномов любые временные ряды в любой отрасли, но если мы не знаем точно, что стоит за динамикой цены, то полиномиальная модель рынка, хорошо описывающая прошлое поведение, может не иметь ни какой предсказательной силы. В данной научной работе описаны основные функции аппроксимации, помогающие при вычислении экономических и статистических задач и различных других данных, с использованием программного продукта Microsoft Excel. Изложены основы построения графиков функций и линии тренда, охарактеризована аппроксимация, показаны возможности программы Microsoft Excel для решения экономических задач. Список литературы: 1. Калиткин Н.Н.Аппроксимация: Численные методы.

Пособие для вузов / Под ред. — М.: «Информационные системы в экономике», 2008. Аппроксимация в Excel — Электронный ресурс — Режим доступа. — URL: (дата обращения ) 3. Аппроксимация: Применение в экономике. — М.: «Аппроксимация», 2005.